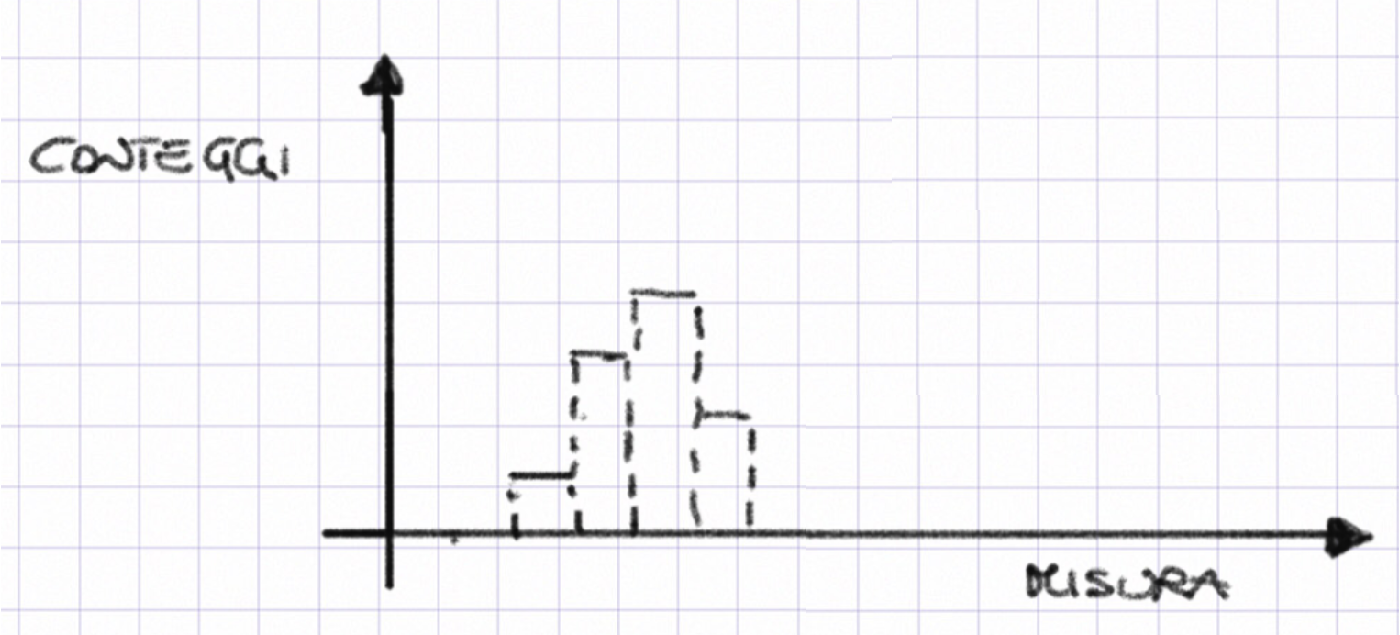
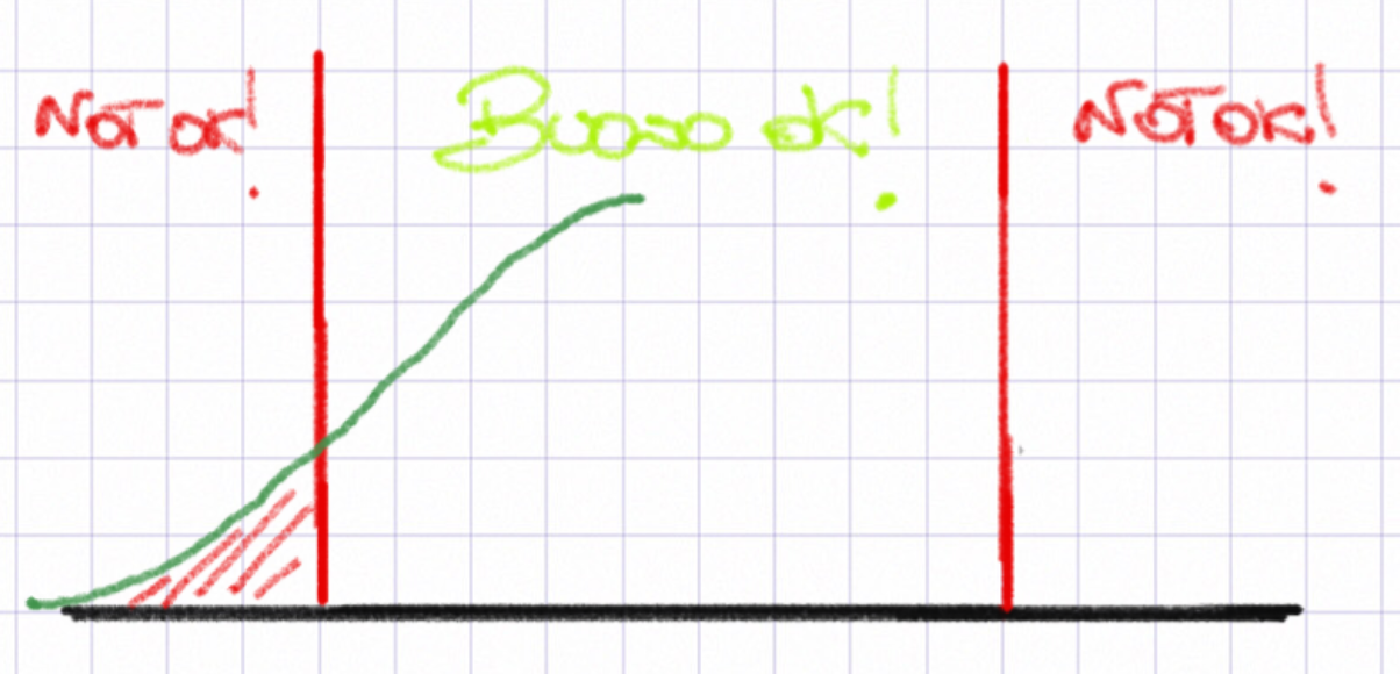
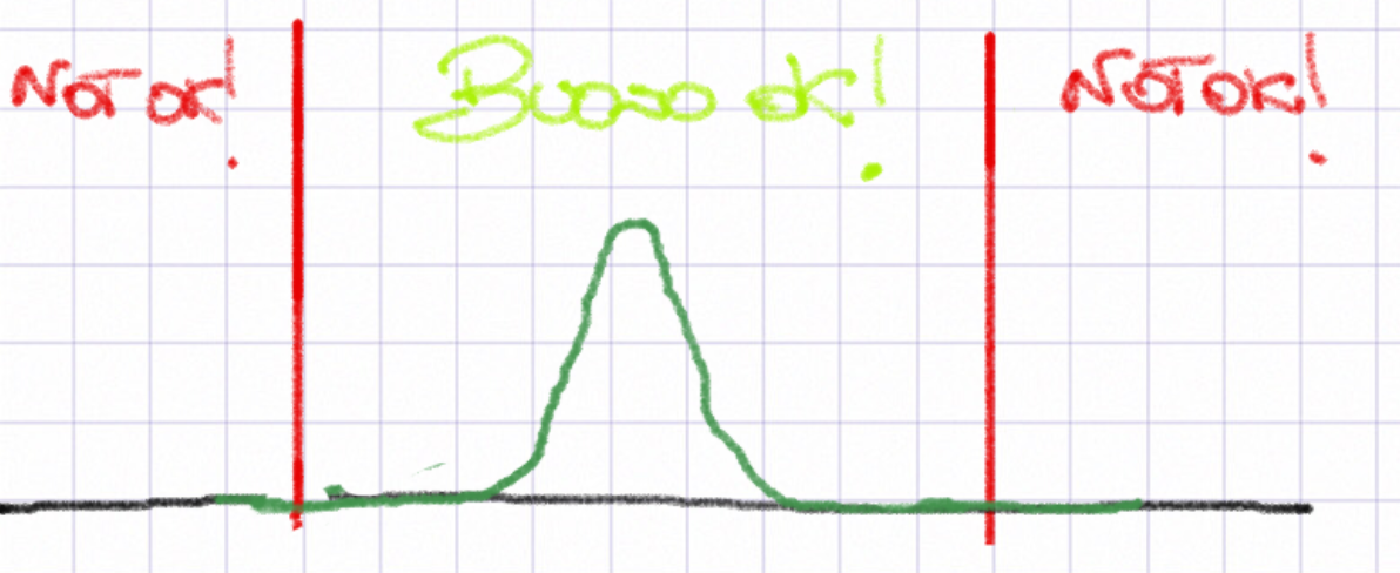
valutiamo il processo
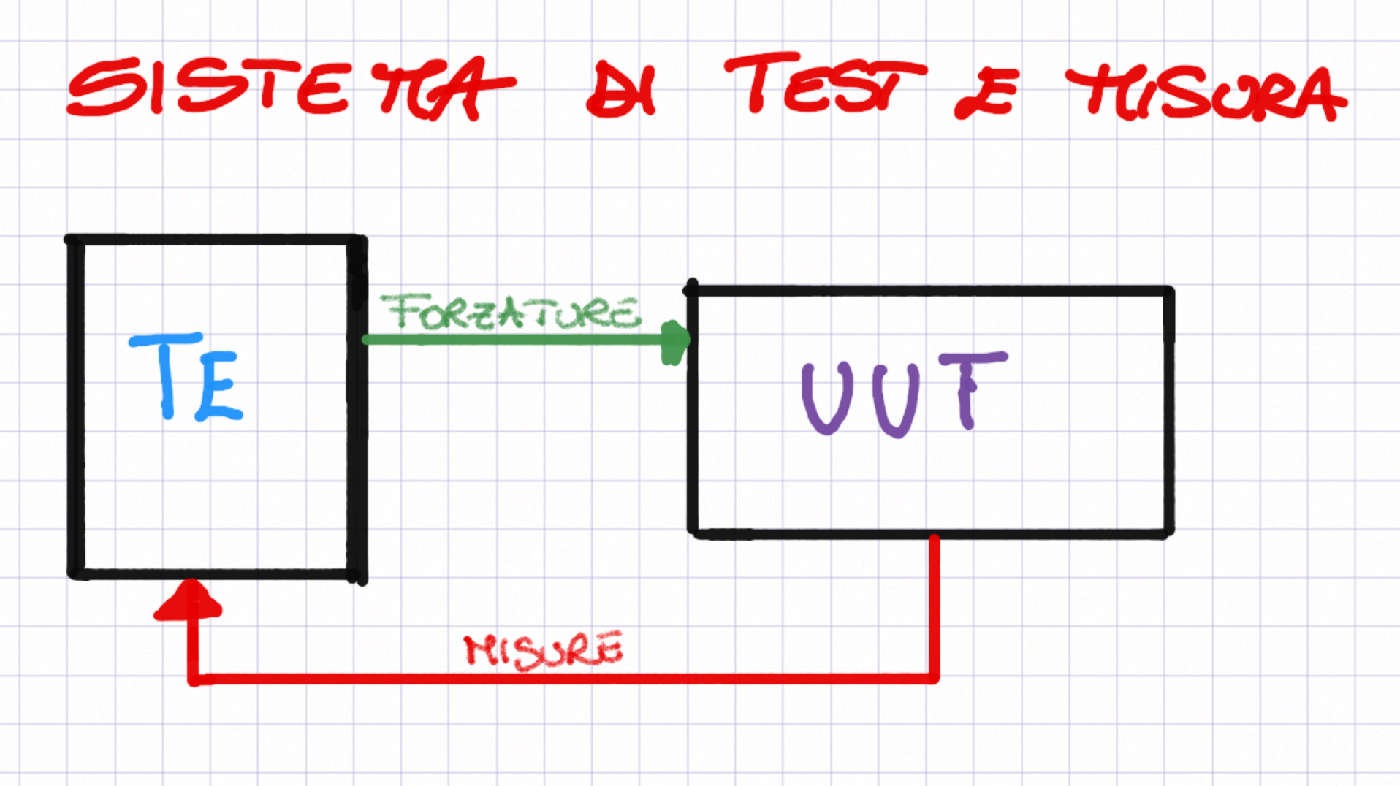
consideriamo un generico processo di produzione e test.
dal reparto di produzione provengono le "unità" e il reparto di test li collauda effettuando sul sistema "forzamenti" e "misure" di vario genere.
un generico TE (test equipment) forza l'unità (UUT Unit Under Test) per misurarne alcuni suoi parametri.